- - -
I. Principes et postulats
PREMIER POSTULAT
Postulat de réfutation de référentiel absolu ou privilégié (réfutation de l'éther).
"Il n'y a pas de référentiel galiléen absolu."
Deux corollaires s'imposent immédiatement:
a) "Les lois de la physique restent les mêmes par changement de référentiel galiléen."
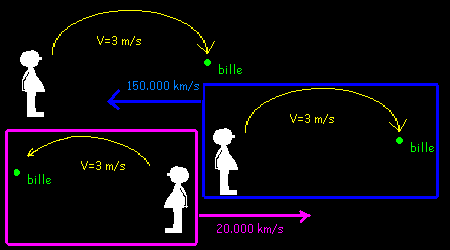
b) "Les effets de la physique sont symétriques par permutation de référentiel galiléen."
Prenons par exemple les exemples suivants, avec Vo=0.6c
Nous ne détaillons pas comment on obtient les contractions et dilatations relativistes ici, mais nous le ferons plus loin;
simplement, les choses dites ici sont énoncées à titre d'exemple pour appuyer la notion relativiste de symétrie universelle
1

2

3

_____
Postulat de réfutation du présent absolu.
Ce postulat reprend l'idée de Poincaré et d'Einstein selon laquelle il n'était peut-être pas logique
de dire que deux événements séparés par une distance, avaient une simultanéité absolue.
C'est la notion d'anisochronie universelle; et la notion de "présent propre", de" simulatanéité propre"
est relative et dépend de la position géométrique de l'observateur dans un référentiel.
Ainsi cette montre placée sur cette table, et cette horloge placée sur la cheminée, ne pourront jamais être "absolument" accordées.
La distance étant de trois mètres entre elles, chacune avance sur l'autre d'un temps T=x.Et
(ou T=x/c), soit ici 10 nanosecondes: c'est la notion simple d'écart-temps(Et) spatial local.
"Il n'y a pas de simultanéité endoréférentielle absolue."

Quatre nouveaux corollaires apparaissent
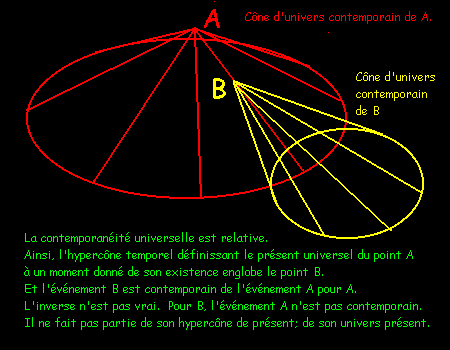
a) "Chaque point constitutif d'un référentiel galiléen se créé pour lui-même
un univers temporel unique qui prend l'aspect géométrique d'un hypercône de simultanéité propre."
b) "La notion de simultanéité endoréférentielle n'est pas symétrique."
c) "Les vitesses observables dans un endoréférentiel galiléen ne sont jamais les vitesses réelles."
d) " En tout endoréférentiel galiléen, il existe une vitesse observable infranchissable
qui va s'étendre à toutes les particules et toutes les propriétés de la physique."
Il suffit de remplacer la vitesse réelle Vr par une valeur infinie
On a Vo=Vr/sqrt(1+Vr^2/c^2)=1/sqrt[(1/Vr^2)+(1/c^2)]
Soit si Vr=Oo ; Vo=c

Un corps, ou une information, se déplaçant infiniment vite dans un référentiel, va, par conséquent, se déplacer infiniment vite dans tous.
Dès lors, il aura partout une vitesse observable de c.
Par suite logique, la vitesse limite observable dans un référentiel galiléen est un invariant par changement de référentiel.
Cela va nous être d'une utilité fondamentale pour retrouver les transformations de Lorentz
et donner la loi d'addition générale de vitesses relativistes.

_____

_____
DES SUITES DE CETTE INVARIANCE DE LA VITESSE DE LA LUMIERE PAR CHANGEMENT DE REFERENTIEL:
Premier étonnement: Relativité du temps par changement de référentiel.
On utilise un petit wagon qu'on va déplacer à une vitesse relative de Vo=0.6c.
On déplace ce wagon de gauche à droite, et on le considère carré sur toutes ses bases,
chaque face ayant 3.10^8m de coté.
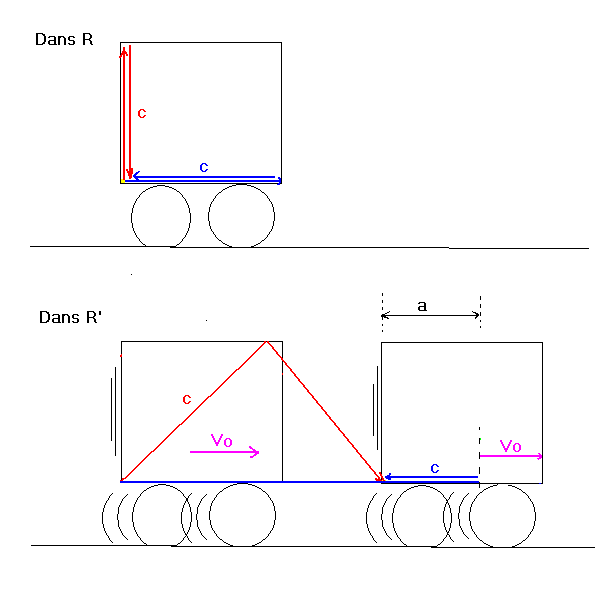
Près de la paroi gauche, on fait partir un flash du bas vers le haut,
où il est reflété sur le bas par un miroir.
L'observateur du wagon va alors noter une seconde pour l'aller, et une seconde pour le retour.
L'observateur laissé sur la voie, va, lui, puisque la vitesse de la lumière est invariante
par changement de référentiel galiléen, percevoir différemment les intervalles de durées.
_____
On a:
h=c.To
et D=c.To'
et aussi D^2=h^2+Vo^2.To'^2 (Pythagore).
Soit encore: (c.To)^2+(Vo.To')^2=(c.To')^2
soit c^2.To^2=To'^2(c^2-Vo^2)
ou To^2=To'^2.(1-Vo^2/c^2)
---------
Soit To'=To/sqrt(1-Vo^2/c^2)

-------
C'est à dire que pour l'observateur externe,
la durée de l'événement"flash-retour du flash"sera de 2.5 secondes dans (R').
C'est la notion de dilatation des temps.
__________________________
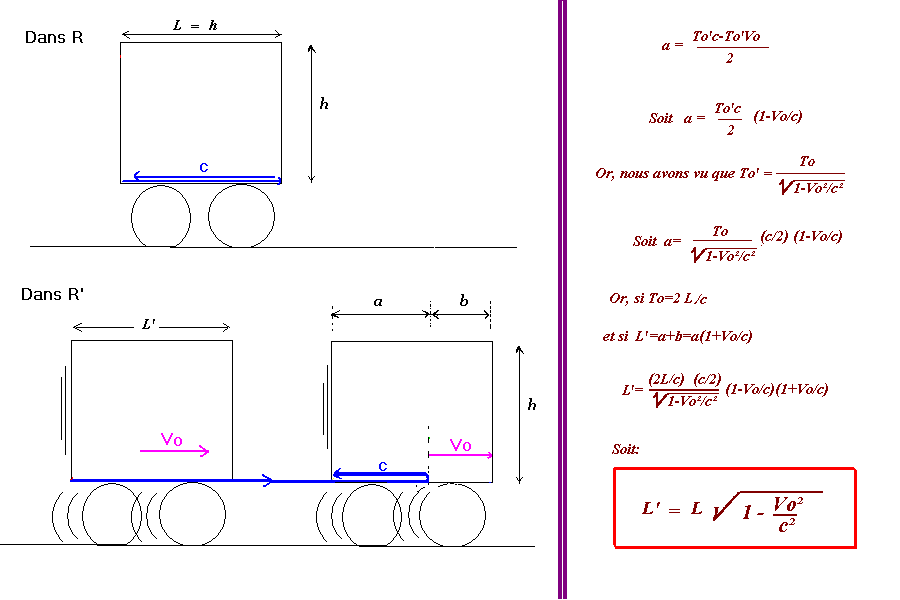
Seconde surprise: Relativité des distances par changement de référentiel.
On va faire partir, cette fois, le flash dans le sens de la marche, et non vers le haut,
c'est à dire le long du plancher du wagon, de gauche à droite,
puis le faire revenir en contre-sens, sur le coin gauche en bas.
L'observateur du wagon trouve la même chose que dans la première tentative,
c'est à dire une durée de deux secondes entre les deux évéments, puisque le wagon est carré
et que ses longueurs valent toutes x=3.10^8m.
Pour l'observateur externe, qui perçoit lui, 2.5 secondes (sinon c'est absurde),
la distance parcourue par la lumière doit être facilement déterminable: D=To'.c=7.5.10^8m
De même que la distance parcourue d par le wagon durant ce temps: d=Vo.To'
On détermine aussi la longueur a du retour lumineux dans R'qui est a=(D-d)/2
On a:
a=(D-d)/2=(c.To'-Vo.To')/2=(To'.c)(1-Vo/c)/2
x'=a(1+Vo/c)
D'où x'=(To'.c/2)(1+Vo/c)(1-Vo/c)=(To'.c/2)(1-Vo^2/c^2)
Or, x=To.c/2 et To'=To/sqrt(1-Vo^2/c^2)
Soit x=To'.sqrt(1-Vo^2/c^2)(c/2)
et x'=To'.(1-Vo^2/c^2)(c/2)
-------
Soit x'=x.sqrt(1-Vo^2/c^2)
-------
Ici, x'=2.4.10^8m
C'est la notion de contraction relativiste des distances.
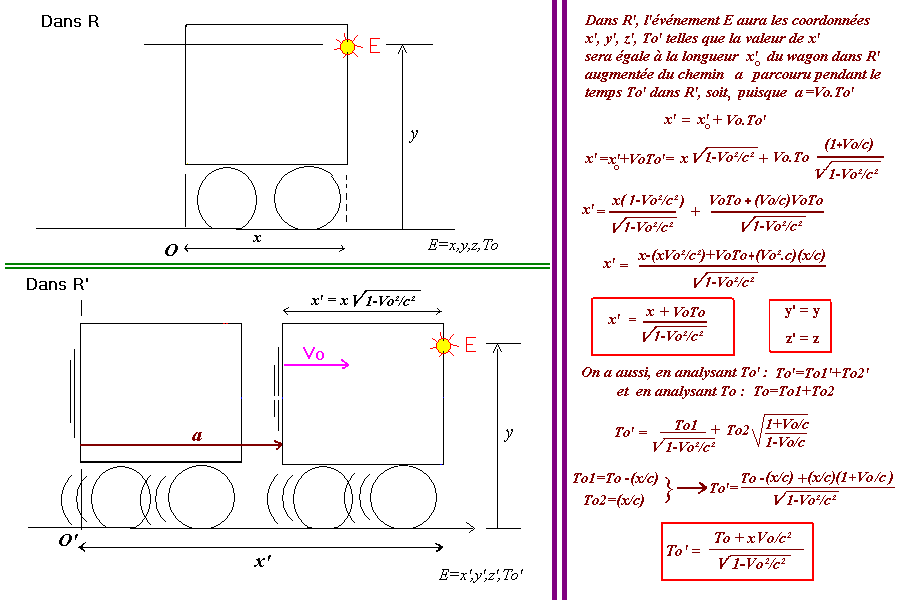
Nous allons poursuivre avec l'idée de lancer un signal électromagnétique de la paroi gauche du wagon
jusque la paroi droite, dans le sens de la marche, et de n'étudier que cet aller simple.

On en déduit alors les transformations de Lorentz (en analysant les temps To et To') en deux parties distinctes
où la deuxième partie correspond à chaque fois au temps observable que met la lumière partant de O ou de O'
pour joindre les deux abscisses dans chaque référentiel