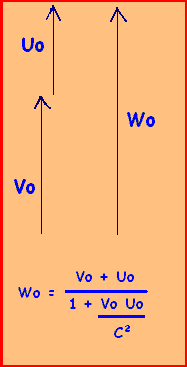
A noter qu'en vitesses réelles, cette équation devient:
Wr=Vr.sqrt(1+Ur^2/c^2) + Ur.sqrt(1+Vr^2/c^2)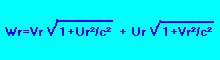



- - - - -
Pour les vitesses retrojetées, on a: Tapp=Tr.sqrt[(1+Vo/c)/(1-Vo/c)]
et aussi: Tapp'=Tapp.sqrt[(1-Uo/c)/(1+Uo/c)]

Soit Tapp'=Tr.sqrt[(1+Vo/c)/(1-Vo/c)].sqrt[(1-Uo/c)/(1+Uo/c)]

Or, on a aussi: Tapp'=Tr.sqrt[(1+Wo/c)/(1-Wo/c)]

Soit: [(1+Vo/c)/(1-Vo/c)].[(1-Uo/c)/(1+Uo/c)]=[(1+Wo/c)/(1-Wo/c)]

D'où: Wo=(Vo-Uo)/(1-Vo.Uo/c^2) CQFD



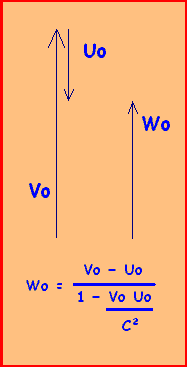
Equation qui devient en vitesses réelles
Wr=Vr.sqrt(1+Ur^2/c^2)-Ur.sqrt(1+Vr^2/c^2)




_ _ _ _ _

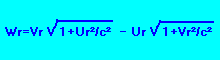
Pour les vitesses transversales, les additions se font selon un protocole différent.
On peut retrouver de plusieurs façons différentes comment déterminer la valeur d'une vitesse résultante de ce type.
Elles sont assez simples, et nous ne les détaillons pas toutes ici.
Quoi qu'il en soit, soit en prenant les vitesses réelles, les vitesses observables
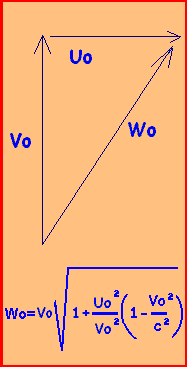
Wo=sqrt[Vo^2+Uo'^2] avec Uo'=Uo.sqrt(1-Vo^2/c^2)
ou en pratiquant comme çi-dessus, avec les temps apparents, on obtient toujours:

Wo=Vo.sqrt[1+(Uo^2/Vo^2)(1-Vo^2/c^2)]

On retrouve encore ce résultat en passant par les vitesses réelles.
Dans le référentiel R une vitesse Vr est notée.
Le référentiel R' note, lui, Ur pour la vitesse transversale...
Soit, si nous mesurons cette vitesse avec une montre de R, Ur"=Ur.sqrt(1+Vr^2/c^2)

Nous appliquons pythagore: Wr=sqrt(Vr^2+Ur"^2)
Soit Wr=Vr.sqrt[1+(Ur^2/Vr^2)(1+Vr^2/c^2)]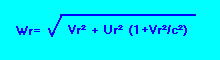



Ce qui revient à la même chose puisque Wo=Wr/sqrt(1+Wr^2/c^2)



_ _ _ _ _

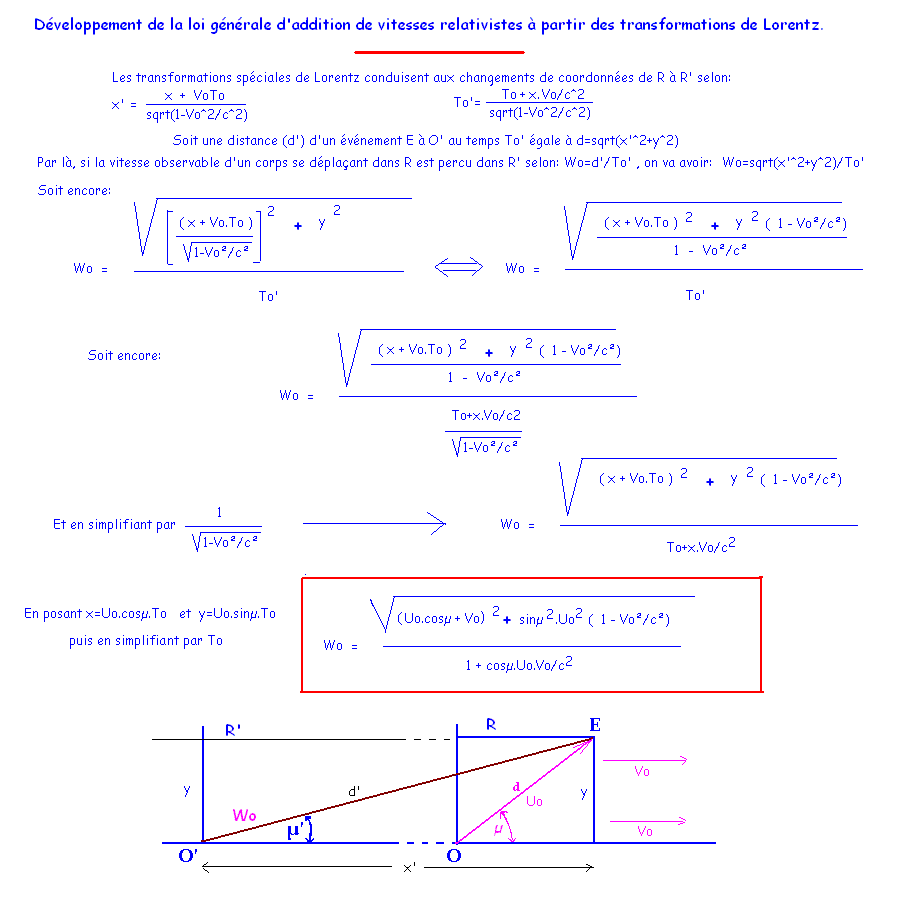
Nous allons donner, en passant, la loi d'addition générale de vitesses relativistes,
et nous montrerons plus tard comment on la retrouve très aisément grâce aux transformations de Lorentz.




---------