De la nature de la simultanéité

VII. Le difficile problème de la simultanéité

- - - - - - - - - - -
On fait se mouvoir, sur une voie ferrée, un wagon virtuel de longueur Lr=10 mètres,
à la vitesse de cent quatre vingt mille kilomètres par seconde (Vo=0.6c).

On place au milieu de ce wagon un individu Y, et, au bord de la voie, un autre individu X (chef de gare).

Deux autres observateurs sont proposés, et placés comme suit:

- Un observateur X' est placé dans le référentiel R de l'observateur X,
mais beaucoup plus loin de la voie que lui, en position d'observateur télétransverse fixe.

- Un observateur Y' est placé dans le référentiel du wagon, qu'il suit, mais de façon télétransverse aussi.

En sorte que, les deux référentiels se mouvant, Y finit par croiser X, et Y' finit par croiser X'.

Le wagon est doté de sortes de pare-choc avant et arrière bien apparents, et se déplace de gauche à droite.

On fait alors tomber sur ce wagon, trois éclairs envoyés comme suit:
- Un éclair A qui tombe sur le pare-choc arrière, et sur la voie juste sous lui.
- Un éclair B qui tombe, de même manière, sur le pare-choc avant, et sur la voie juste sous lui.
- Un éclair E qui tombe au milieu de train, sur l'observateur y et sur l'observateur x, en plein croisement.

On admet que, par principe, ces trois éclairs sont simultanés pour l'observateur télétransverse X'.

Je veux montrer que, selon ce que j'ai toujours dit, la notion de simultanéité n'était nullement relative
par changement de référentiel, mais que deux événements simultanés dans un référentiel l'étaient aussi dans tout autre,
et que les défauts de synchronisation viennent des positionnements de points dans les référnetiels,
et non des référentiels eux-mêmes.

"La simultanéité est un phénomène constant par changement de référentiel:
si deux événements A et B sont simultanés dans R, ils le sont aussi dans R'
pour peu qu'on ai pris soin de faire coïncider les deux points de chaque référentiel
au moment où les simultanéités apparaissent pour l'un des deux points."

Nous allons donc maintenant nous intéresser, très précisément, à ce que va percevoir l'observateur X'
(position télé-transverse dans R, loin du talus).

X' dans le référentiel R va voir passer un train qui ne mesure plus 10 mètres, mais 8 mètres.
C'est la notion logique de contraction des longueurs: Lo=Lr.sqrt(1-Vo^2/c^2).

Maintenant, SIMULTANÉMENT POUR LUI, les trois éclairs ont lieu.

L'un tombe en A (pare choc et voie), l'autre en B (pare choc et voie)
et le troisième au milieu (sur X et sur Y).



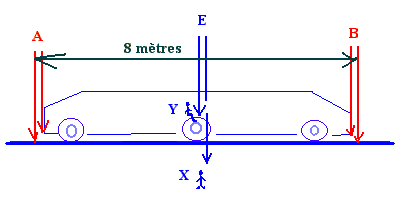
Évidemment, pour X', la distance entre A et B, qui est de 8 mètres dans R va induire qu'il y a aussi
quatre mètres entre A et X, quatre entre A et Y, quatre X et B, et quatre Y et B.

Continuons:
Ayant parlé de X' sans avoir d'autre chose à ajouter, on s'intéresse maintenant à ce que va percevoir X,
qui au contraire de X', et bien que dans le même référentiel, est, lui, positionné tout près de la voie.

Pour X, la distance entre les deux éclairs devra être de huit mètres aussi,
c'est logique puisqu'il est dans le même référentiel que X'.

MAIS chacun accordera que la perception des trois éclairs ne sera pas simultanée,
dans le sens où A et B (qui le seront, eux) parviendront à X après l'éclair de E.
Soit avec 1.33333.10^-8secondes de retard.
A cet instant de X, qui perçoit l'événement E, en même temps que y le croise (centre du wagon)
A et B n'existent pas encore;
ils n'existeront, simultanément pour X, que dans 13.333 nanosecondes environ.

Or, la longueur apparente du wagon, pour X, à cet instant où E a lieu et où Y le croise,
est bel et bien de 10 mètres à gauche, et de 2.5 mètres à droite; je ne refais pas les démonstrations.



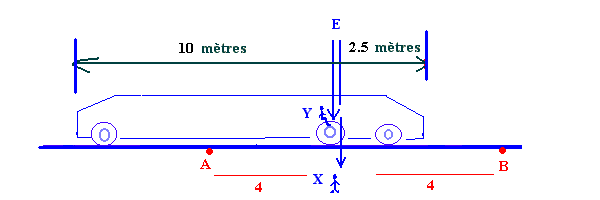
Je rappelle simplement que X voit la partie gauche du wagon s'approcher à Vapp'=1.5c,
et la partie droite le fuir à Vapp=0.375c.

C'est à dire qu'à cet instant, pour X, le pare-choc arrière va encore devoir parcourir
10m-4m= 6 mètres à la vitesse apparente Vapp=1.5c;
et le pare-choc avant 4m-2.5m=1.5 mètre à la vitesse apparente de 0.375c.

Cela va faire que 1.3333.10^-8 seconde plus tard, pour X, le pare choc avant arrive pile en B,
et le pare-choc arrière pile en A.
A cet instant, les éclairs A et B, séparés de huit mètres, sont simultanés.
Mais Y, au centre du wagon est déjà passé, et se trouve alors à 1.5 mètres sur la droite de X.




C'est d'une grande simplicité, et, là dessus, et jusqu'ici, je crois, tous les relativistes sont d'accord avec moi.

Nous allons maintenant nous intéresser à la vision des choses perçues par Y et par Y'.

Dans le référentiel du wagon, où Y est assis, en son milieu,
et que Y' observe de loin, en position télétransverse, le train mesure 10 mètres.
Pour Y, placé au milieu du train, et croisant X, la logique physique est maintenue, et l'instant où E tombe sur lui,
correspond à l'instant où X le croise, car un chien ne devient pas un chat par changement de référentiel.

A cet instant, la partie CX vaut 4.sqrt[(1-Vo/c)/(1+Vo/c)]=2mètres
et la partie XD vaut 4.sqrt[(1+Vo/c)/(1-Vo/c)]=8mètres

Reste donc trois mètres à C à gauche pour trouver A, et trois à D à droite pour trouver B.
Nous nous souvenons que C se déplace à 0.375c et D à 1.5c.
Nous aurons donc l'évolution suivante:
Y percoit E au moment où X passe, puis B 0.666.10^-8secondes plus tard,
puis A seulement 2.666.10- 8secondes plus tard.

Le piège, c'est de considérer que cette absence flagrante de simultanéité
est due à une inconstance de simultanéité par changement de référentiel.
C'est faux, et ici, le décalage vient du fait que dans le référentiel de R, Y a bougé,
alors que X n'a pas bougé dans R, et que, justement,
nous avions admis que la simultanéité était parfaite sur la transverse XX', mais non ailleurs.
Cette non simultanéité est donc positionnelle et non référentielle.

X est à 0.75m à gauche lorque Y perçoit B, et 3m à gauche lorsqu'il perçoit A

Il ne peut donc y avoir de simultanéité des deux événements A et B pour Y,
puisque cela est basé sur la seule droite XX'

Pas plus qu'il n'y aura simultanéité pour Y' qui percevra également les flashs dans l'ordre E, B, A
mais cela du à la position de Y'

"La simultanéité isopositionnelle est invariante par tout changement de référentiel;
deux entités présentent au même endroit (conjonction) ont le même hypercône d'univers"

et que le référentiel soit galiléen, ou en rotation uniforme, voire en mouvement accéléré,
cela n'y change strictement rien.


_____________

Nous pouvons aussi présenter le problème différemment.