VII. Physique corpusculaire relativiste

Notion de quantité de mouvement.
La quantité de mouvement est classiquement définie comme le produit de la vitesse réelle d'un corps
dans le référentiel qui l'observe par la masse de ce corps...
En physique relativiste, on ne doit pas déroger à cette règle:
p=m.Vr dans tous les cas de figure.
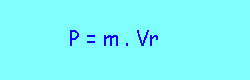
Or, nous avons dit que la vitesse réelle n'était pas la vitesse observable.
Si nous voulons calculer une quantité de mouvement au moyen de la vitesse observable d'un corps,
nous devons alors poser: p=m.Vo/sqrt(1-Vo^2/c^2)
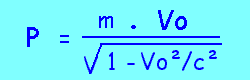
Exemple: calculer la quantité de mouvement d'un proton de masse 938 MeV/c^2 se déplaçant à Vo=0.6c
dans le référentiel du laboratoire.
p=m.Vr=m.Vo/sqrt(1-Vo^2/c^2)
p=703.5 MeV/c
_ _ _ _ _
Notion d'énergie corpusculaire.
L'énergie gloabale d'un corps (somme de l'énergie cinétique et de l'énergie de masse)
est donné selon la relation suivante: E=mc^2[Vr/Vo]
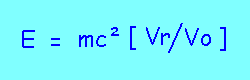
Soit aussi: E=mc^2.sqrt(1+Vr^2/c^2)
ou encore:
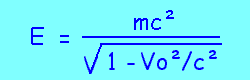
Si nous voulons connaitre l'énergie cinétique d'une particule, il nous faut alors poser Ec=E-Eo
Or, Eo=mc^2 , donc Ec=mc^2[sqrt(1+Vr^2/c^2) - 1]
Ec=mc^2.[sqrt(1+Vr^2/c^2)-1]
ou Ec=mc^2[{1/sqrt(1-Vo^2/c^2)}-1]
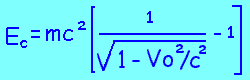
L'énergie cinétique du proton va donc être: E=938MeV/c^2*(0.25)=234.5MeV/c^2
A noter que la simplification des équations donnant E et p conduit à:
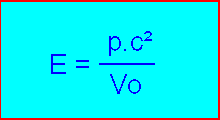
De là, on a encore, en remplaçant Vo par Vr:
E=[pc²/Vr].sqrt[1+Vr²/c²]
D'où en passant au carré:
E²=[p².c^4/Vr²]+[p².c^4.Vr²/(Vr².c²)]
Ce qui se simplifie en:
E²=p².c^4/Vr² + p²c²
Or, p=m.Vr ---> Vr=p/m
D'où en ôtant Vr:
E²=m².c^4+p².c²
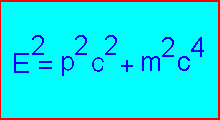
Et, en donnant l'impulsion en fonction de l'énergie cinétique (Ec), les deux équations possibles:
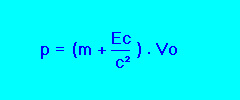
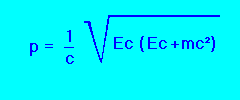
________________
Problème fréquent:
On envoie un positon (électron positif) contre un électron.
Le choc annihile les deux corpuscules avec libération totale de leur énergie.
On a alors l'équation suivante:
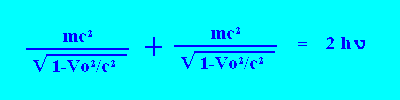
________________
EXPLICATION DE L'EFFET CHERENKOV
On bombarde un milieu liquide d'indice n avec des électrons (masse m=0.51MeV/c^2)
de grande énergie E et doté d'une vitesse Vo, constante dans R, et supérieure à celle de la lumière dans R'.
On constate alors la production d'ondes lumineuses dans le milieu, prenant l'aspect de cônes de Cherenkov
dont le sommet est à chaque instant la particule, et dont le semi-angle est alpha.
On calcule l'énergie minimale nécessaire ainsi:
Vitesse de la lumière dans l'eau c'=c/n=0.75c
Energie nécessaire pour produire un électron devant atteindre cette vitesse limite dans l'air
E=mc^2/sqrt(1-Vo^2/c^2)
_______
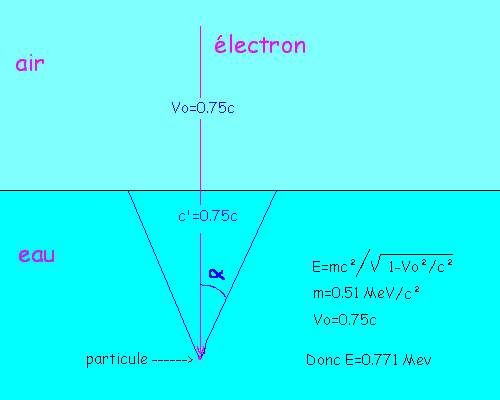
On voit donc que l'énergie nécessaire est ici de 0.771 MeV
____
Le référentiel barycentrique relativiste
_____
Définition:
On appelle référentiel barycentrique R de deux référentiels relativistes R' et R",
le référentiel se plaçant entre ces deux référentiels prédéfinis
de telle façon que la vitesse observable relative soit égale de R vers R' et R vers R".
Utilité:
Ce référentiel relativiste a une importance capitale dans le traitement des problèmes relativistes
et en particulier dans les calculs d'énergie, de quantité de mouvement et d'angle d'éjection
des particules relativistes qui se télescopent, mais aussi pour beaucoup d'autres problèmes relativistes.
Physique:
Nous savons que la loi d'addition de vitesses relativistes longitudinales est donnée par:
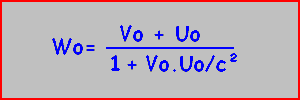
De là, il vient que le référentiel barycentrique R va se trouver être défini par Vo (qui est aussi Uo) dans:
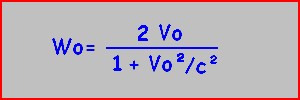
Soit aussi:
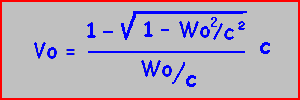
Exercice:
On bombarde une plaque métallique très fine avec des électrons de masse m=0.51 MeV/c^2 et de vitesse Vo=0.968c
L'électron incident percute alors un électron au repos dans R,
et les deux électrons sont projetés dans R selon un angle donné sur l'axe initial.
En mécanique classique, l'angle formé par les deux électrons devrait être égal à un droit,
c'est à dire 45° de part et d'autre de l'axe incident.
En mécanique relativiste, les choses n'en vont pas ainsi, et on remarque que l'angle vaut, environ, une soixantaine de degrés.
Explication:
En mécanique hachelienne, nous avons dit lors du troisième corollaire du second postulat
que les vitesses observables dans un référentiel donné n'étaient jamais les vitesses réelles;
mais plutôt que Vo=Vr/sqrt(1+Vr^2/c^2), ou, à l'inverse, que Vr=Vo/sqrt(1-Vo^2/c^2)
Ainsi, l'électron incident à une vitesse observable de Vo=0.968c, mais une vitesse réelle de 3.85734c environ.
Nous savons, en outre, que la conservation de l'énergie globale se fait sous la forme:
E=mc^2.sqrt(1+Vr^2/c^2)+mc^2=2*mc^2.sqrt(1+Ur^2/c^2)
[ équation que l'on peut encore écrire sous la forme:
E=mc^2/sqrt(1-Vo^2/c^2)+mc^2=2*mc^2/sqrt(1-Uo^2/c^2) ]
Soit aussi:
mc^2.[sqrt(1+Vr^2/c^2)+1]=2*mc^2.sqrt(1+Ur^2/c^2)
Si Vr vaut 3.857339114c, alors Ur=2.283c et Uo=0.916c
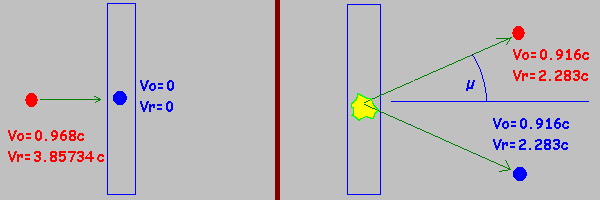
On a par ailleurs, en se plaçant au niveau du référentiel barycentrique:
Vo=Uo=0.7738c environ (de par l'équation donnée plus haut).

On a donc affaire à deux électrons qui vont se télescoper avec chacun la vitesse de 0.7738c dans R, et qui vont être éjectés perpendiculairement,
gardant ainsi la même énergie et la même quantité de mouvement dans ce référentiel-là.

Il suffit alors, pour connaître la vitesse relative dans R" (ici le labo) des deux électrons sortant,
de faire une simple addition des vitesses transversales, comme j'en ai déjà donné l'équation:
Wo=sqrt(Vo^2+Uo^2-Uo^2.Vo^2/c^2).
On a alors: Wo=sqrt(2*0.7738c^2-0.7738c^4/c^2)
On retrouve alors Wo=0.916c, ce qui confirme bien la valeur trouvée tout à l'heure en passant par la conservation des énergies,
mais montre aussi, en passant, que l'équation proposée pour les additions de vitesses transversales est correcte.
Calcul de l'angle d'éjection des électrons dans le référentiel du laboratoire:
Dans le laboratoire, l'électron s'éloigne de la plaque métallique à vitesse Ur=1.221603826
alors qu'il s'éloigne (dans R barycentrique) à Uo=0.738c
On a alors tg µ = coté opposé/côté adjacent = 0.773811782/1.221649385 = 0.633415603
Soit µ=32°21'
Une autre façon de calculer cet angle est de prendre la quantité de mouvement
La conservation de celle-ci dans le laboratoire avant et après le choc conduit à poser:
p=m.Vr=m.Ur/2
Soit Ur=Vr/2=1.928669557c.
Nous avons vu que la vitesse d'éjection des électrons était Vr=2.283c selon un angle µ,
et nous avons maintenant la composante longitudinale sur l'axe qui est Ur=1.928669557c
Soit cos µ =côté adjacent/hypothénuse=~1.92867/2.283=0.84480752
Soit µ=32°21'

