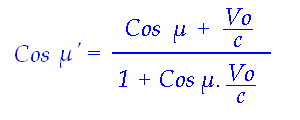1. L'invariance de la vitesse de la lumière par changement de référentiel
En connaissant maintenant la relation qui lie, dans un référentiel donné, la vitesse observable et la vitesse réelle, il devient facile de déterminer
la valeur de la plus grande vitesse observable possible dans ce même référentiel; et donc, dans tous, puisque nous plaçons maintenant,
selon Einstein, tous les référentiels galiléens de l'univers sous le même pied d'égalité (notion de covariance générale).

2. La dilatation des durées et la contraction des longueurs
L'invariance de la vitesse de la lumière par changement de référentiel va conduire l'observateur transverse O' fixe dans R',
et qui voit passer transversalement un train fixe dans R à une impression de dilatation des temps selon les principes suivants:

et à une contraction des longueurs selon:
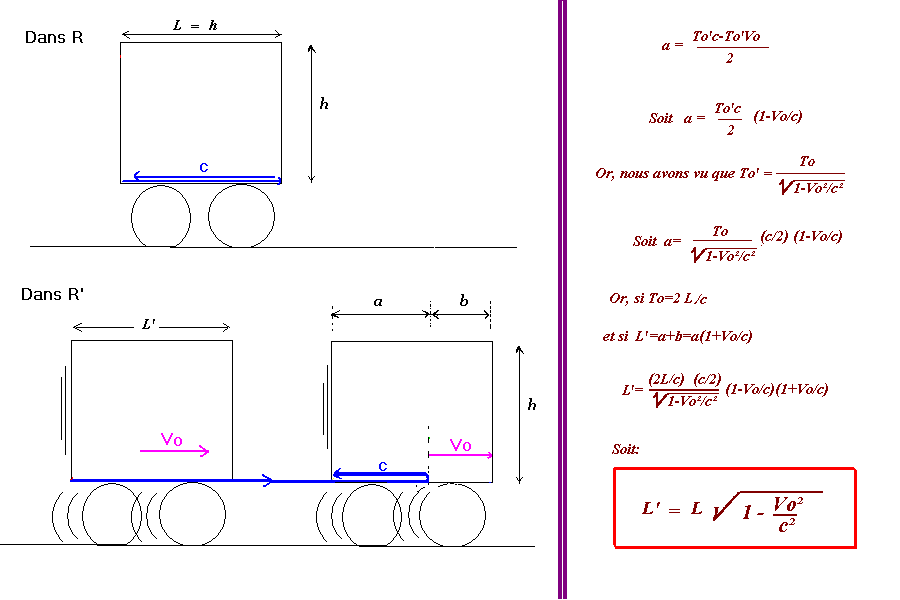
Nous soulignons une nouvelle fois que, chez Einstein, ces dilatations de temps et ces contractions de distances sont symétriques:
pour la personne assise dans le wagon, c'est le temps du quai qui se dilate, et c'est la longueur des rails qui se contracte.
Nous allons pouvoir donner l'équation générale entre la longueur apparente d'un objet dans un référentiel par rapport à sa longueur réelle.
Il suffit de prendre alors la relation classique liant une longueur observable et une longueur apparente,
et d'introduire la longueur réelle en place de l'observable pour avoir une relation directe.
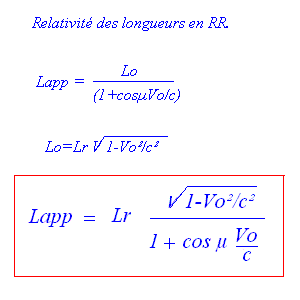
On voit alors que si l'objet fuit ou approche longitudinalement les équations se résument à:
Lapp'=Lr.sqrt[(1-Vo/c)/((1+Vo/c)] et Lapp"=Lr.sqrt[(1+Vo/c)/(1-Vo/c)]
3. Les transformations de Lorentz
Nous allons poursuivre avec l'idée de lancer un signal électromagnétique de la paroi gauche du wagon
jusque la paroi droite, dans le sens de la marche, et de n'étudier que cet aller simple.

On en déduit alors les transformations de Lorentz (en analysant les temps To et To') en deux parties distinctes
où la deuxième partie correspond à chaque fois au temps observable que met la lumière partant de O ou de O'
pour joindre les deux abscisses dans chaque référentiel
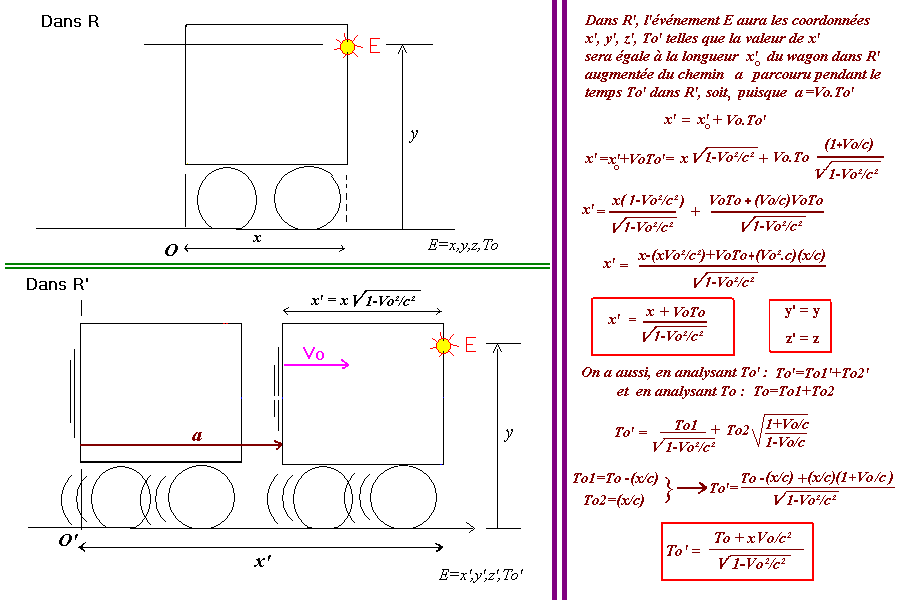
Les tranformations inverses devenant:
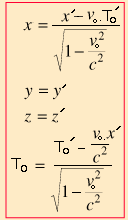
4. Loi générale d'addition de vitesses relativistes
Une fois les transformations de Lorentz obtenues, on peut alors déduire la loi générale d'addition de vitesses relativistes comme suit:
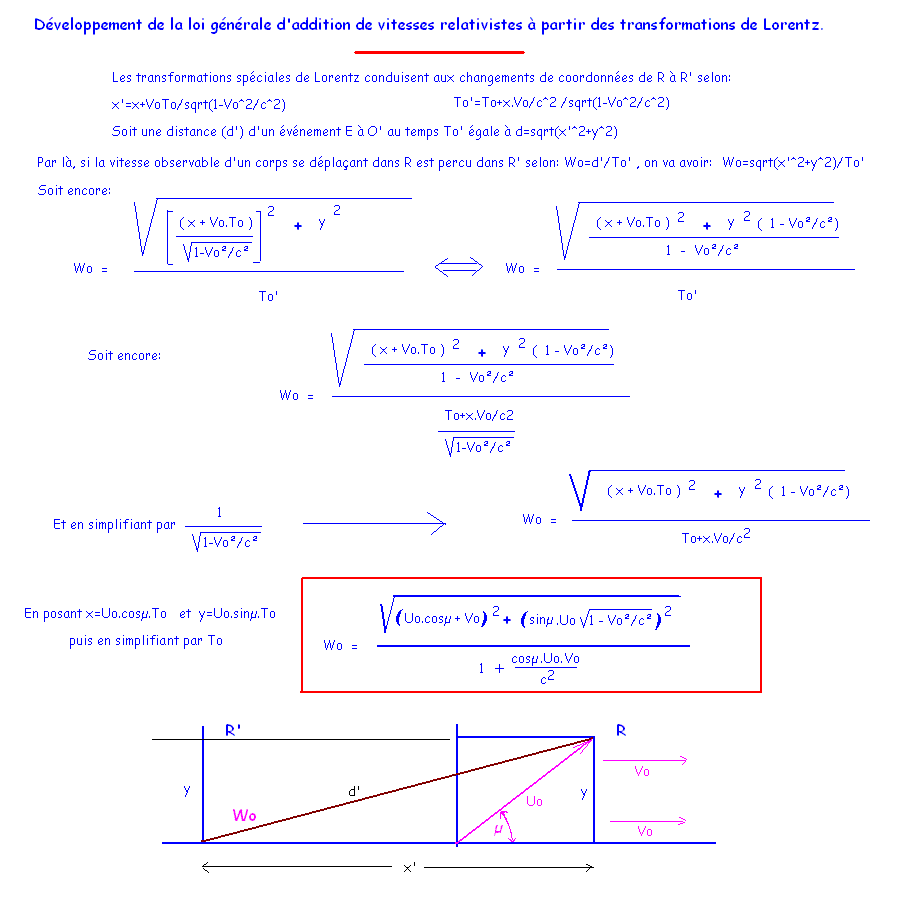
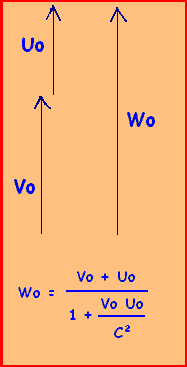
Nous pouvons alors prendre les trois cas particuliers suivants que sont les additions longitudinales, les soustractions longitudinales,
et, pour finir, les additions de vitesses orthogonales.
Ce qui est la même chose que, si nous utilisons les vitesses réelles:
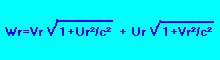
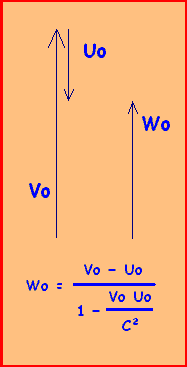
Ce qui est la même chose que, si nous utilisons les vitesses réelles:
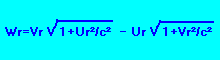
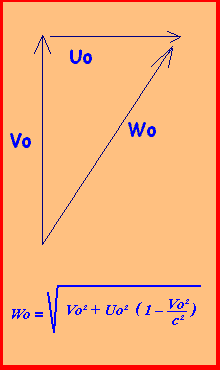
Ce qui est la même chose que, si nous utilisons les vitesses réelles:
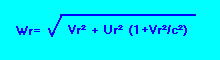

On obtient alors l'angle µ' puisque cosµ=Uo'/Uo et cosµ'=Wo'/Wo et donc que cosµ'=cosµ.(Wo'/Wo).(Uo/Uo'), soit:
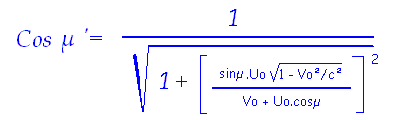
On peut aussi travailler en vitesses réelles en utilisant les conversions appropriées:

5.Déduction et étude des fréquences pulsatiles relativistes
On peut alors déterminer facilement les fréquences pulsatiles apparentes par rapport aux fréquences pulsatiles réelles.
Néanmois, il faut faire très attention de ne pas confondre cette notion avec les fréquences électromagnétiques,
qui ne varient pas de cette façon par changement de référentiel, mais selon ce que nous déterminerons plus loin.

6.Déduction et étude des fréquences électromagnétiques relativistes
Pour ce qui est des fréquences et longueurs d'onde électromagnétiques, on peut raisonner comme suit:
L'énergie d'un corps se déplaçant dans un référentiel donné est comme: E=mc^2[Vr/Vo]=mc^2.sqrt(1+Vr^2/c^2)=mc^2/sqrt(1-Vo^2/c^2)
Or, on peut se mettre à l'échelle d'un photon, et, donc, poser hv'=hv/sqrt(1-Vo^2/c^2)
Il vient alors que la fréquence observable du photon dans R' sera proportionnelle à celle de R comme v'=v/sqrt(1-Vo^2/c^2)
Pour la longueur d'onde, on a directement, puisque Lambda=c/v: Lambda'=Lambda.sqrt(1-Vo^2/c^2)
Or, si l'on s'imagine un corps croisant l'axe de visée selon un angle µ sur cet axe, on a: Lambda_app=Lambda_o (1+cosµ.Vo/c)
Et donc, puisque Lambda_o=Lambda_r.sqrt(1-Vo^2/c^2): --->Lambda_app=Lambda_r.sqrt(1-Vo^2/c^2)/[1+cosµ.Vo/c]
Ici, il faut bien prendre garde que la longueur d'onde mesurée est celle qui est envoyée dans la direction de la visée,
et non la longueur d'onde apparente observée par l'observateur qui est, elle:
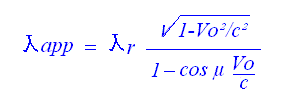
Soit une fréquence électromagnétique égale à:
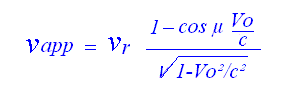
A noter les cas particulier d'un mobile se déplaçant longitudinalement et qui émet un photon vers l'observateur.
Selon le sens du déplacement, on a:
Lambda_app'=Lambda_r.sqrt[(1+Vo/c)/(1-Vo/c)] (fuite de l'observateur)=red-shift,
Lambda_app"=Lambda_r.sqrt[(1-Vo/c)/(1+Vo/c)] (approche de l'observateur)=blue-shift
Enfin, puisque l'émission du photon se fait à la vitesse de la lumière, soit Uo=c, on a une émission selon l'angle µ':