1. La réfutation de la simultanéité absolue et le principe d'anisochronie universelle
Le premier grand principe de la théorie de la relativité restreinte a été donné au tout début du XX° siècle par le brillant mathématicien français Henri Poincaré.
En effet, dès 1904, pour tenter d'expliquer certaines expérimentations physiques aux conséquences étonnantes ou imprévues, voire contradictoires,
comme celle de l'expérience interférométrique de Michelson et Morley, Henri Poincaré va proposer un postulat relativiste absolument nouveau et révolutionnaire
selon lequel: "des événements physiques se produisant sur des théâtres différents bâtissent des systèmes de simultanéité différents."

On pensait pourtant, depuis l'antiquité, qu'un même calendrier valait pour tout l'univers; et que, par simple déduction d'esprit, des événements simultanés pour un observateur étaient simultanés pour tous les observateurs de l'univers, sans que personne n'eut songé à contredire, tant l'idée paraissait évidente et inattaquable.
Bref, il semblait qu'il était tout à fait licite de dire que si deux événements étaient simultanés pour A, ils l'étaient aussi, forcèment, pour B.
Pour mieux dire, que tous les théâtres du monde possédaient le même système de simultanéité.
Or,c'est cette notion même que Poincaré remettait maintenant en cause.
Mais si l'on postule cela, et on se rend compte du courage et de la hardiesse de Poincaré, non seulement c'est l'un des principaux piliers de la physique classique
de Newton et de Galilée qui s'effondre, puisque le temps n'est plus perçu comme quelque chose d'absolu, indépendant de la position de l'examinateur,
mais encore, de causes en effets logiques: les notions de durées absolues, de vitesses absolues, et même les notions de longueurs et de distances, éclatent.
Plus rien ne va alors tenir debout.
Ainsi, si nous prenons l'exemple de deux événements se produisant en des endroits différents A et B (on peut choisir la Tour de Londres et la Tour Eiffel),
la notion de simultanéité étant relative à la position de l'observateur: deux événements simultanés pour A ne seront, généralement, plus simultanés pour B.
Admettons simplement qu'un physicien se place à mi-distance entre Paris et Londres, et qu'il envoie, par ici, à Londres, et par là, à Paris, un signal quelconque.
Au moment où la Tour de Londres (A) et la Tour Eiffel (B) percoivent le message, elles réenvoient une réponse électromagnétique vers le physicien central,
qui, lui, va, en principe, et suivant la logique, percevoir les deux réponses A et B simultanément.
Notre physicien central M aura donc une double réception parfaitement simultanée des deux événements, et on pourra dire que, pour lui,
les deux réponses auront eu lieu "en même temps". Mais revenons à ce qui se passe pour les deux tours:
Qu'en est-il pour la Tour de Londres, et pour la Tour Eiffel? Chacune des deux tours reçoit le signal renvoyé par l'autre tour avec un net retard!
L'expérimentation montre alors que le retard est de delta_t = x/c et qu'il est symétrique.
On peut un instant accuser l'une des tours d'avoir mal renvoyé son signal, c'est à dire avec un certain retard, mais cela ne tient pas:
l'effet étant symétrique pour les deux tours; et l'observateur central M étant certain de la simultanéité des réponses.
Ainsi pour chacune des tours, la réponse de l'autre tour retarde toujours, quoi qu'on fasse, de delta_t = x/c, alors que ces deux réponses sont simultanées pour M.
Bref, pour conclure, trois observateurs différents ont des notions très différentes de la simultanéité de deux événements s'étant produits sur des théâtres éloignés.
Bien sûr, à la lecture de ce qui vient d'être dit ici, le lecteur se pose depuis quelques secondes, une question obligatoire:
"Peut-être que tout simplement toutes ces mesures sont normales, et simplement dues au fait que la vitesse de la lumière n'est pas infinie:
il peut donc paraitre logique que cette vitesse étant finie, un décalage temporel puisse être mesuré, expliquant, de surcroit, la parfaite symétrie des mesures."
Mais en disant cela, le lecteur va montrer qu'il n'a pas encore tout à fait compris l'idée géniale de Poincaré.
Pour Poincaré, l'idée primordiale est bien celle de l'anisochronie de chaque théâtre du monde par rapport à tout autre théâtre pris en référence;
il pensait que s'il y avait réellement une simultanéité absolue, il devait bien y avoir de cela, dans notre monde, une sorte de "confirmation externe" expérimentale;
et que si l'on parvenait à montrer qu'un corps pouvait avoir un effet ou une action (mécanique, gravitationnelle, électrique, électromagnétique)
infiniment rapide sur un autre corps, la notion de simultanéité absolue serait alors prouvée.
Or, cette "confirmation externe" n'existait pas; rien ne semblant pouvoir dépasser c; et, pour Poincaré,comme plus tard pour Einstein,
cela était probablement du à la nature-même de notre "espace-temps" et de ses systèmes de simultanéité, et non à la défaillance technique
des appareils de mesure comme le croyait encore le physicien Albert Michelson, lorsqu'il parlait de l'échec apparent de son appareillage interférométrique
(pourtant très précis et tout à fait sophistiqué et qu'il avait concu pour mesurer de la vitesse de la terre dans l'espace absolu).
Bien: la notion d'anisochronie universelle étant maintenant posée comme principe physique vrai, nous allons chercher à mesurer celle-ci.
Expérimentalement, il semble bien qu'elle soit égale à un écart-temps (Et) de 3.33 nanosecondes par mètre dans le vide (c'est, en fait, l'inverse de c).
Cela veut dire qu'un observateur qui voit se déplacer un mobile M, sur un mètre, ne pourra jamais le voir se déplacer en un temps supérieur à cette constante.
Le temps réel étant nul si le déplacement a été instantané, le temps observable sera pourtant non nul et égal à To=Tr+Et, soit 3.33 nanosecondes.
L'objet qui s'est pourtant déplacé infiniment vite (cas du photon) en un temps propre nul, semble s'être déplacé à la vitesse de la lumière pour l'observateur fixe.
Mais si l'idée de Poincaré est correcte, et nous pensons qu'elle l'est, il doit bien y avoir une formule générale liant les vitesses réelles aux vitesses observables,
formule qui prendrait en compte ce leurre sur les vitesses par effet d'anisochronie, et, pour mieux dire:
comment peut-on donner la vitesse observable d'un corps par rapport à sa vitesse réelle dans le référentiel qui l'abrite, et réciproquement?
On peut alors résoudre cela très simplement avec un simple pythagoricisme.
Voyons: imaginons que le mobile se déplace en un temps réel (ou, ce qui est la même chose: temps propre) Tr de A à B sur la distance x.
Pour le mobile, placé dans R, et qui notera un temps Tr, il n'y a pas de déplacement. Il est immobile dans R,
et il voit simplement s'écouler un temps Tr. Il n'y a donc pas d'écart-temps supplémentaire à prendre en compte.
Pour l'observateur externe, fixe dans R', il existe, en surcroit, un déplacement AB, noté x,
et par lequel le mobile se déplace également dans l'anisochronie de AB, anisochronie égale, nous l'avons dit, à delta_T = x/c.
Le temps observable par cet observateur placé en R' va donc dépendre de deux valeurs, l'une le temps réel Tr du mobile,
et l'autre, l'écart-temps delta_T (anisochronie de Poincaré) existant entre A et B.
La transformée physique de Tr dans R sera alors égale à To dans R' selon le pythagorisme suivant:
(à noter que si Tr=0, To=delta_T; et que si delta_T=0 (objet immobile), To=Tr)
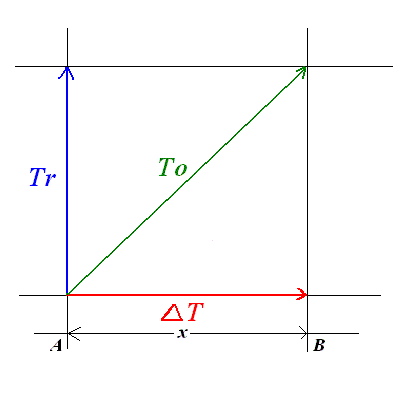
Ainsi, si nous admettons un delta_t(AB) de 3 secondes, par exemple, et un corps qui traverse réellement AB en 4 secondes,
(ou l'inverse delta_t = 4 et T r= 3) eh bien le déplacement sera mesuré comme déplacement effectué en cinq secondes
L'équation s'inverse si nous voulons connaitre le temps propre (connaissant le temps observable). Exemple: delta_t = 3; temps observable To = 5; alors Tr = 4
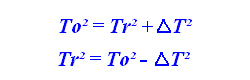
Et, si nous parlons en vitesses et non en temps, puisque les vitesses sont inversement proportionnelles aux temps mesurés:
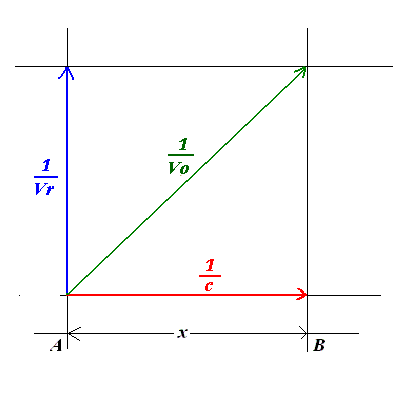
Ce qui conduit facilement à une relation des vitesses réelles aux observables:
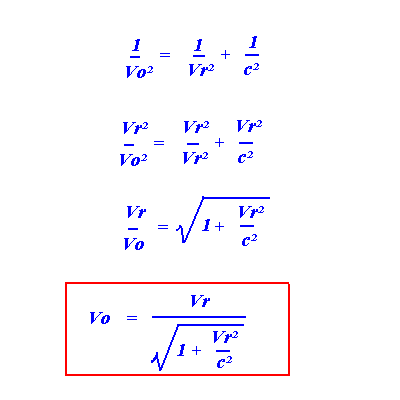
et, évidemment, des vitesses observables aux réelles selon:
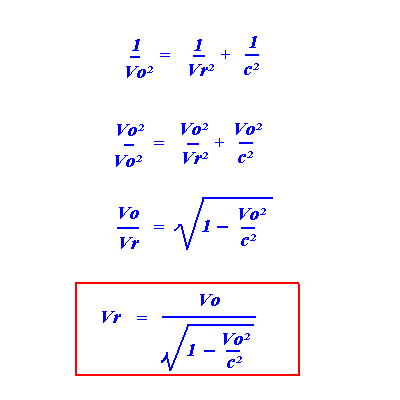
2. Considérations expérimentales relativistes
Nous allons donner deux preuves expérimentales de la valeur de la théorie de la relativité restreinte:
a) Notion relativiste de la quantité de mouvement.
La quantité de mouvement est classiquement définie comme le produit de la vitesse réelle d'un corps dans le référentiel par la masse de ce corps...
Et physique relativiste, on ne doit pas déroger à cette règle:p=m.Vr dans tous les cas de figure.
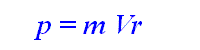
Or, nous avons dit que la vitesse réelle d'un corps dans le référentiel qui la mesurait n'était jamais la vitesse observable.
Si nous voulons calculer une quantité de mouvement au moyen de la vitesse observable d'un corps, nous devons alors poser: p=m.[Vo/sqrt(1-Vo^2/c^2)]
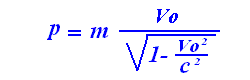
Exemple: calculer la quantité de mouvement d'un proton de masse 938 MeV/c^2 se déplaçant à Vo=0.6c dans le référentiel du laboratoire.
Si nous prenons la vitesse observable du proton, nous n'obtenons pas la quantité de mouvement attendue (p=703.5Mev/c)
mais une quantité de mouvement moindre p=m.Vo=562.8Mev/c.
Or, si nous prenons correctement p=m.Vr=m.[Vo/sqrt(1-Vo^2/c^2)]
p=703.5 MeV/c
b) Notion expérimentale de relativité des vitesses
La durée de vie moyenne des mésons "pi" au repos a pu être déterminée expérimentalement: Tr=2.55.10^-8 s.
Des mésons "pi" sont alors animés d'un mouvement rectiligne de vitesse observable Vo=0.9995c par rapport à un observateur terrestre.
On peut alors penser, avec les lois de la physique galiléo-newtonienne, qu'ils vont parcourir, en moyenne, x=Vo.Tr, soit, environ, x=7.65m.
Or, ce n'est plus le cas si nous prenons le principe de la relativité enseigné par Poincaré et Einstein: la vitesse réelle étant plus grande que prévue,
la distance moyenne parcourue par les corpuscules sera beaucoup plus grande. Soit, vérifié expérimentalement; x=Vr.Tr ~ 242m.
___
3. La réfutation du référentiel absolu et le principe de covariance générale
En tout début du XX° siècle, Albert Einstein, un modeste employé d'un bureau de Berne, va révolutionner la physique en portant plus loin les idées de Poincaré.
Bien sûr, pour Einstein, les principes de Poincaré restent valables, mais, pour lui, il n'y a pas de contrariété réelle entre l'abandon de l'éther
et l'aspect ondulatoire de la propagation lumineuse; il affirme alors que l'idée d'éther n'est tout simplement pas nécessaire, et que la contradiction observée
n'est en fait qu'une contradiction apparente liée à notre mauvaise compréhension de l'espace-temps et nos a priori ancestraux..
Mais ce n'est pas encore le plus important: la grande originalité d'Einstein va être de proposer une physique nouvelle où les contractions de Lorentz
ne sont pas absolues, mais parfaitement symétriques. A posteriori, cela semble assez concordant avec l'idée de réfutation du tout référentiel absolu,
et c'est assez intuitif, mais l'idée nouvelle n'en est pas moins extraordinaire et originale: il y a maintenant un grand principe de symétrie générale:
de même que la tige traversant l'espace à grande vitesse se contracte pour moi, eh bien je me contracte aussi pour elle, et cela, dans les mêmes proportions.
Lorsqu'un individu voit passer un train dans un tunnel, il voit le train plus court que le tunnel, alors qu'ils ont la même longueur à l'arrêt, c'est vrai;
mais pour Einstein, en place de l'observateur placé dans le train, c'est le tunnel qui est plus court, et cela s'explique par le fait
que la simultanéité est une notion propre à chaque observateur. L'un voit par exemple l'avant du train déjà passé à ce bout du tunnel, et l'autre non.
Tous les observateurs ne sont pas dans le même univers spatio-temporel.
Ainsi telle chose peut paraître plus courte ou plus longue selon la position de l'observateur; selon comment on la regarde.
Il en va de même pour deux horloges qui se déplacent l'une par rapport à l'autre, chacune des deux horloges trouve que c'est l'autre qui bat moins vite.
Cela semble, a priori, absurde, mais c'est en fait très proche de l'effet de perspective: quand deux hommes s'éloignent, chacun d'entre eux
voit l'autre apparemment plus petit, et si nous ne nous en formalisons pas trop, c'est parce que nous sommes dès l'enfance habitués à cette évidence.
Cette notion de symétrie, Einstein va l'appeler «principe de covariance générale», c'est à dire qu'il place maintenant tous les référentiels galiléens
sur le même pied d'égalité; et, pour lui, non seulement les lois de la physiques restent les mêmes par changement de référentiel galiléen,
mais mieux: les effets de la physique demeurent symétriques par permutation référentielle.

Bien sûr, beaucoup ont pensé que l'apport d'Einstein sur la relativité restreinte ne fut que très partielle, tant les travaux de Poincaré avaient prédisposé
à la compréhension complète de la théorie, mais il ne semble pas que la notion de symétrie générale ait été proposée par un autre physicien qu'Einstein.
C'est en cela qu'il faut comprendre l'importance formidable de son intuition,
et par là, apprécier toute l'utilité de sa contribution dans l'élaboration de la relativité restreinte.

