III. Le voyageur de Langevin
Le voyageur de Langevin est l'histoire relativiste d'un jumeau qui va quitter son frère terrestre pour effectuer
un long périple dans l'espace au travers de l'espace et du temps.
On admet que ce voyageur part du référentiel terrestre le jour de ses trente ans,
et qu'il laisse là son frère jumeau.
La vitesse observable de la fusée mesurée dans le référentiel terrestre est fixée
à cent quatre vingt mille kilomètres par seconde.
Soit Vo=0.6c.
On cherche alors à déterminer ce qui va se passer si le frère part ainsi pendant dix ans de son temps propre,
puis, ayant assez voyagé, revient à la même vitesse qu'à l'aller,
et selon un trajet quasi rectiligne dirigé vers la terre.
Première constatation, en cohérence avec le principe d'Einstein-Newton:
il n'y a pas de référentiel absolu.
Les deux jumeaux sont, en tout état de cause, placé sur le même plan,
et leurs évolutions doivent rester parfaitement symétriques, dans le respect des lois logiques.
Conservation parfaite et complète du premier principe d'Einstein: il n'y a aucun référentiel privilégié.
Nous savons qu'en outre, les vitesses relativistes observables ne sont jamais les vitesses réelles.
Ainsi, la vitesse réelle, ou vitesse propre du jumeau dans l'espace-temps, est-elle de Vr=Vo/sqrt(1-Vo^2/c^2)
Soit Vr=0.75c
Nous aurons donc un frère qui partira durant une période réelle Tr de 10 ans
vers les étoiles à la vitesse propre de Vr=0.75c.
La distance parcourue sera alors de x=0.75c*10ans=7.5 années de lumière.
Deux questions vont maintenant se poser au lecteur attentif:
- que va percevoir le frère terrestre de ce périple, et comment vont s'organiser les deux phases aller-retour?
- mais surtout, chose plus complexe: que va percevoir le jumeau cosmonaute de son frère resté sur terre?
C'est à ces deux questions que nous allons répondre, en utilisant, par ailleurs, divers mode de vitesses.
A. Perception du voyage par le frère resté sur terre.
Le frère resté sur terre observera l'aller de son jumeau, durant une période qui va devenir:
Tapp=Tr*sqrt[(1+Vo/c)/(1-Vo/c)] soit 20 ans.
C'est la notion simple de dilatation des durées.
Cela veut simplement dire que lorsque le frère des étoiles touchera son aphélie,
là bas à 7.5 années de lumière, sa montre de voyageur notant 10 ans,
hé bien le frère terrestre percevra cela pendant que sa montre à lui marquera 20 ans.
Tout se sera passé comme si la montre du frère des étoiles aura tourné deux fois moins vite.
Nous avons vu que la réfutation de tout référentiel privilégié entraine une symétrie parfaite.
Donc, pour l'autre frère, c'est réciproque, et la montre terrestre lui parait aussi tourner deux fois moins vite.
Revenons au frère terrestre:
Pour le retour, le frère terrestre verra son frère évoluer selon:
Tapp'=Tr*sqrt[(1-Vo/c)/(1+Vo/c)] soit Tapp'= 5 ans.
C'est la notion de contraction des durées.
Premier résultat:
le frère terrestre, pour lui, aura vieilli de 25 ans; alors que le frère des étoiles aura vieilli de 20 ans.
C'est la notion de relativité du temps.
On peut, si l'on veut, se mettre en place du point fixe externe situé exactement à 7.5 années de lumière de la terre.
Que va percevoir ce point?
Eh bien, l'équation s'inverse, et, au total, Tapp=Tr/sqrt[(1+Vo/c)/(1-Vo/c)]=5 ans pour l'aller.
Et donc Tapp=Tr/sqrt[(1-Vo/c)/(1+Vo/c)]=20 ans pour le retour.
Soit, pour ce point là, situé dans le même référentiel que le jumeau terrestre, la même durée totale pour le voyage,
mais avec deux phases différentes...

B. Perception du voyage par le frère cosmonaute.
Ici, nous entrons de plein pied dans la fantastique musicalité du concept relativiste.
Nous avons dit que celui-là, qui voyage, percevrait un aller de 10 ans, et un retour de 10 ans.
Mais que percevra-t-il de son frère resté sur terre durant ces périodes?
La même chose que son frère vis à vis de lui, c'est à dire dilatation des durées à l'aller
(il voit le temps de la terre tourner plus lentement : effet Doppler de fuite),
et contraction des durées au retour (il voit les horloges de la terre tourner deux fois plus vite).
On aura donc, pendant les dix ans de l'aller, une dilatation des durées de:
Tapp=Tr[sqrt[(1+Vo/c)/(1-Vo/c)]]=5 ans.
C'est à dire que le présent du virement du cosmonaute sera, pour lui, synchrone du moment où,
sur la terre, l'horloge du frère notera cinq ans.
Et pour le retour: Tapp'=Tr[sqrt[(1-Vo/c)/(1+Vo/c)]]=20 ans
Donc, pendant son retour vers la terre, le cosmonaute verra celle-ci vieillir de 20 ans
pendant que lui vieillira de 10 ans.

Soit un accord des deux frères qui comptent: 25 ans pour l'un; 20 ans pour l'autre.
Il n'y a donc aucun paradoxe, et les effets sont très simples et d'une logique implacable.
Ce qui est admirable dans ce concept nouveau,
c'est que, toujours, l'équation reste toujours à l'identique pour les deux protagonistes.
Les deux jumeaux se voient réciproquement vieillir moins vite à l'aller, et selon la même équation:
T(apparent)=T(réel).sqrt[(1+Vo/c)/(1-Vo/c)] à l'aller;
et réciproquement vieillir plus vite au retour:
T(apparent)=T(réel).sqrt[(1-Vo/c)/(1+Vo/c)] au retour;
- - - - - - -
C. Le voyageur de Langevin en mode bi-cinétique.
Admettons maintenant que le voyageur modifie sa vitesse durant le voyage.
Au lieu de voyager à Vo=0.6c dans le référentiel terrestre (soit une vitesse réelle de Vr=0.75c), ce voyageur,
enhardi par une technologie performante et le maintien impeccable des moteurs nucléaires pendant l'aller,
décide de forcer sa vitesse jusque 0.8c au retour...
Soit une vitesse réelle Vr=1.333333c
Comment les choses se passeront-elles?
En fait, il n'y a pas trop à s'en inquiéter, et les équations restent évidemment les mêmes.
L'aller se passera évidemment de la même façon que dans le cas précédent,
et le retour se passera ainsi:
Pour le jumeau des étoiles:
Tr=x/Vr -----> Tr=7.5 années lumières/1.3333333c
Tr=5.625ans.
Soit un voyage total de 15.625ans.
Pour le jumeau terrestre:
Tapp=Tr[sqrt(1-Vo/c)/(1+Vo/c)]=5.625/3=1.875ans
Soit un voyage total durant 21.875 ans.
Pour le jumeau des étoiles regardant la montre terrestre:
En fin d'aller, nous avons dit qu'il touchait l'aphélie en Tr=10 ans
et voyant l'autre montre marquer 5 ans.
Pour le retour, il va voir la montre terrestre tourner trois fois plus vite
et noter Tapp=Tr[sqrt(1+Vo/c)/(1-Vo/c)]=5.625*3=16.875ans.
La durée mesurée sur la montre terrestre va donc lui paraitre:
5+16.875ans=21.875ans.
Il y a adéquation complète avec le frère terrestre.
C'est d'une précision parfaite.
Chacun des protagonistes va s'accorder sur le fait que le frère des étoiles aura vieilli moins vite,
sans qu'aucun paradoxe ne vienne jamais s'imisser dans le concept relativiste.
Tous les calculs présentés ici peuvent également être présentés en mode vitesses réelles...
Tapp=Tr.[sqrt(1+Vr^2/c^2)+Vr/c ]
Tapp'=Tr.[sqrt(1+Vr^2/c^2)-Vr/c ]
L'univers relativiste est d'une cohérence fantastique.
- - - - -
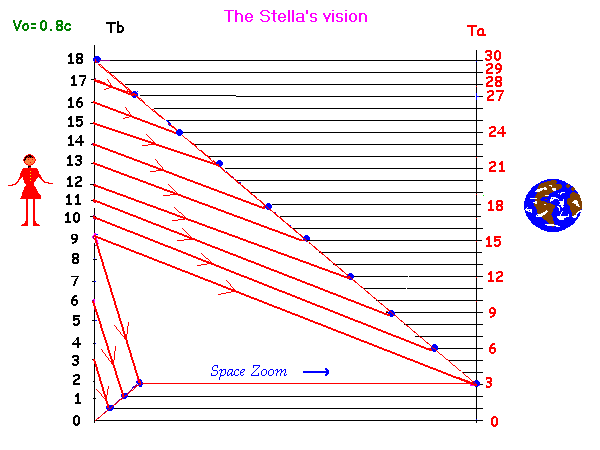
Nous allons maintenant donner les concordances de temps par un diagramme aller-retour en vitesse Vo=0.8c
Nous prenons un temps propre aller et retour de 18 ans (9+9) pour le frère des étoiles.
Nous voyons que, là encore, les deux protagonistes sont d'accord pour dire que le frère des étoiles
a vieilli moins vite, au total, que le frère terrestre, et dans les mêmes proportions.
Voilà ce que percevra le jumeau terrestre de l'heure de son frère.
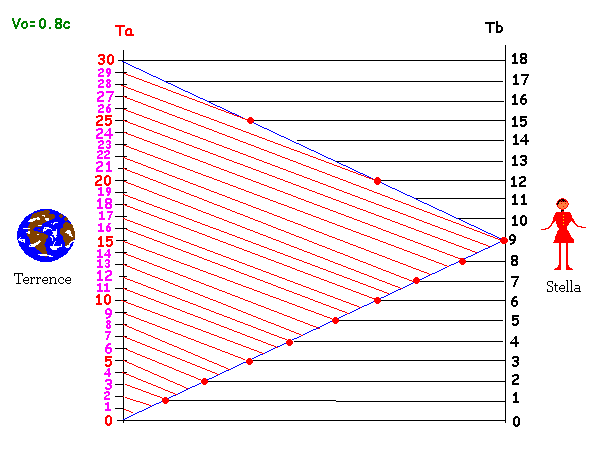
VISION DESCRIPTIVE DES CHOSES OBSERVEES PAR LE FRERE TERRESTRE
(huit schémas explicatifs)








VISION DESCRIPTIVE DES CHOSES OBSERVEES PAR LE JUMEAU DES ETOILES
(dix schémas explicatifs)










Voilà maintenant ce que percevra le jumeau des étoiles de l'heure du frère terrestre durant les phases aller-retour.
On remarque qu'à l'instant Tb=9 ans, ce jumeau "saute de référentiel".
C'est cela qui va induire, pour lui, une fracture du parallélisme des droites de correspondances.