IV. Relativité des longueurs et des longueurs d'ondes
Nous allons maintenant nous intéresser aux longueurs relativistes.
Un observateur regarde une fusée s'éloigner à Vo=0.6c en translation longitudinale dans l'espace,
et elle émet deux bips électromagnétiques séparés de 20.10^-8sec.
On demande de calculer le temps apparent terrestre et la distance parcourue par la fusée entre ces deux bips.
On a, pour un observateur placé derrière la fusée:
Tapp=20.10^-8*sqrt[(1+Vo/c)/(1-Vo/c)]=40.10^-8sec.
Un observateur placé devant de la fusée mesurerait
deux bips distants de Tapp'=40.10^-8*sqrt[(1-Vo/c)/(1+Vo/c)]=10.10^-8sec.
Un observateur placé assez loin et transversalement (position télétransverse)
observerait un délai de Tapp"=Tr/sqrt(1-Vo^2/c^2)=25.10^-8sec.
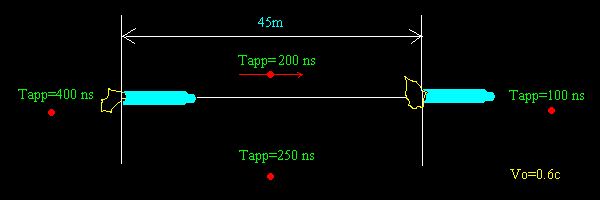
La distance parcourue est la même pour les quatre observateurs:
x=Vapp'.Tapp'=1.5*3*10^8*10*10^-8= 45 mètres
x=Vapp.Tapp=0.375*3*10^8*40.10^-8= 45 mètres.
x=Vr*Tr=0.75*3*10^8*20*10^-8= 45 mètres.
x=Vo*To=0.6*3*10^8*2.5*10^-8= 45 mètres.
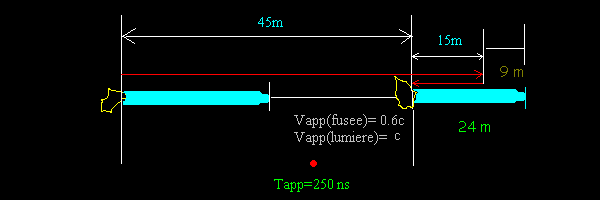
A l'instant de l'émission du premier bip, et lancé de la queue de la fusée, on émet un rayon lumineux
vers l'avant de la fusée, le rayon est réfléchi, et revient à son point originel.
La fusée mesurant 30 mètres dans son référentiel,
le temps de l'aller-retour est mesuré en T=x/c=60/3*10^8= 20*10^-8 sec.
Pour le référentiel postérieur, on aura évidemment 40*10^-8 sec.
La longueur du trajet pour la fusée sera de 60 mètres, c'est à dire:x=c*To=60 mètres, pour l'aller-retour.
Le trajet de ce même rayon dans l'espace sera pour l'observateur postérieur
(la vitesse apparente d'un rayon lumineux en fuite est 0.5c):
x=Vapp.Tapp=0.5*3*10^8*40*10^-8=60 mètres.
On va donc avoir, dans le même temps apparent de 40.10^-8secondes,
une fusée se déplaçant à Vapp=0.375c sur 45 mètres,
et un rayon lumineux se déplacant à 0.5c sur 60 mètres.
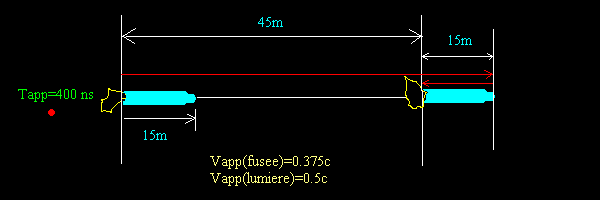
Le retour de la lumière est infiniment rapide dans tous les référentiels
La lumière a donc parcouru 75 mètres.
60 d'aller (à 0.5c) et 15 de retour (infiniment vite).
Il n'y a pas d'autre solution que de dire que, dans le référentiel postérieur,
la longueur apparente de la fusée est de 15m.
----
Passons maintenant à la position de l'observateur antérieur, qui, placé devant elle, la voit arriver vers c.
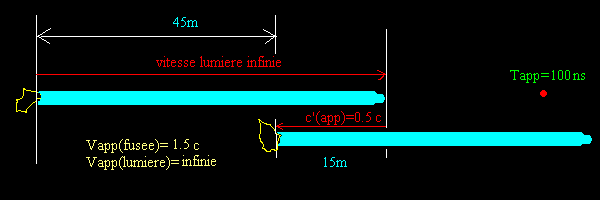
Il voit un rayon lumineux se déplacer infiniment vite vers lui,
puis repartir à 0.5c (comme toujours pour une lumière qui fuit)
sur 15 m et en 100 nanosecondes.
----
Enfin, plaçons nous au niveau de l'observateur positionné de façon télétransverse,
c'est à dire transversalement et assez loin pour que les angles de visée soient considérés
comme étant à peu près parallèles