Théorie de la relativité de l'espace et du temps.

- - -

V. Formules de transformations de Lorentz

On considère deux référentiels galiléens (R):O,x,y,z et (R'):O',x',y',z' d'axes respectivement parallèles.

L'axe O'x' glisse maintenant le long de l'axe Ox de (R) à vitesse Vo constante mesurée dans (R).

L'homogénéité de l'espace et du temps conduit à des transformations reliant
les coordonnées (x,y,z,t) d'un événement E dans (R)
aux coordonnées (x',y',z',t') de ce même événement mesuré dans (R').

On synchronise les horloges de (R) et de (R') à l'heure t=t'=0 lorsque les origines O et O' coïncident.








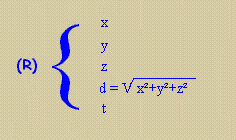
On a la géométrie spatio-temporelle suivante:




Avec a/Vo=h'/c
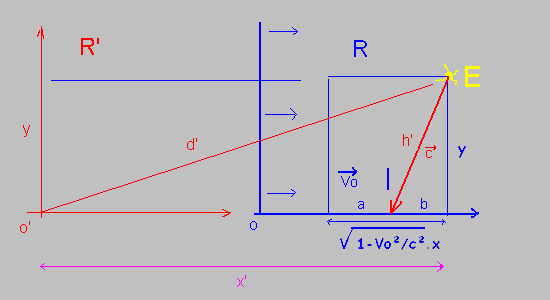
a+b=sqrt(1-Vo^2/c^2).x
h'^2=b^2+y^2
x'=(Vr.t)+b
Les inconnues du systèmes sont a, h', b et x'.

De là, nous déterminons To' par les trois premières équations, puis x'par la dernière.

1. Nous allons déterminer la composante temporelle référentielle To' par rapport à To.

On a: a= x'-b = sqrt(1-Vo^2/c^2).x - sqrt[(1-Vo/c)/(1+Vo/c)].x = (Vo/c).sqrt[(1-Vo/c)/(1+Vo/c)].x

Soit, si Vo.dTo'= a alors dTo'=a/Vo et donc dTo'=sqrt[(1-Vo/c)/(1+Vo/c)].(x/c)

Alors que To'=t/sqrt(1-Vo^2/c^2)-dTo'

Soit To'=t/sqrt(1-Vo^2/c^2) - sqrt[(1-Vo/c)(1+Vo/c)](x/c)

Soit To'=[To+(x/c)]/sqrt(1-Vo^2/c^2) - sqrt[(1-Vo/c)(1+Vo/c)](x/c)

Soit To'=[To+(x/c)-(x/c)+(Vo.x/c^2)]/sqrt(1-Vo^2/c^2)

Soit To'=[To+(Vo.x/c^2)]/sqrt(1-Vo^2/c^2)

2. Détermination de la composante x' dans R'.

x'= sqrt(1-Vo^2/c^2).x + Vo.t/sqrt(1-Vo^2/c^2) - dTo'.Vo

x'= sqrt(1-Vo^2/c^2).x + Vo.t/sqrt(1-Vo^2/c^2) - Vo(dTo-x.Vo/c^2)/sqrt(1-Vo^2/c^2)

x'= sqrt(1-Vo^2/c^2).x + Vo.t/sqrt(1-Vo^2/c^2) - Vo.dTo/sqrt(1-Vo^2/c^2) + x.(Vo^2/c^2)/sqrt(1-Vo^2/c^2)

x'= Vo.t.sqrt(1-Vo^2/c^2) + x.(1-Vo^2/c^2)/sqrt(1-Vo^2/c^2) + x (Vo^2/c^2)/sqrt(1-Vo^2/c^2) -Vo.dTo/sqrt(1-Vo^2/c^2)

x'= x/sqrt(1-Vo^2/c^2) + Vo (T-dTo)/sqrt(1-Vo^2/c^2)

x'= x/sqrt(1-Vo^2/c^2) + Vo.To/sqrt(1-Vo^2/c^2)

On a donc les transformations linéaires suivantes:
x
y
z
d=sqrt(x^2+y^2+z^2)
To
t=To+d/c

x'= [1/sqrt(1-Vo^2/c^2).x+[Vo/sqrt(1-Vo^2/c^2)].To
y'=y
z'=z
d'=sqrt(x'^2+y'^2+z'^2)
To'=[To+(Vo.x/c^2)]/sqrt(1-Vo^2/c^2)
t'=To'+(d'/c)




La transformée inverse devenant:





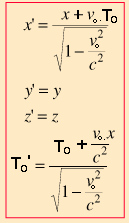
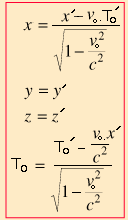
On peut aussi donner la transformée des temps dits "apparents" en O et O', c'est à dire temps "direct-live":
Soit, pour la transformée t' en O':




---------

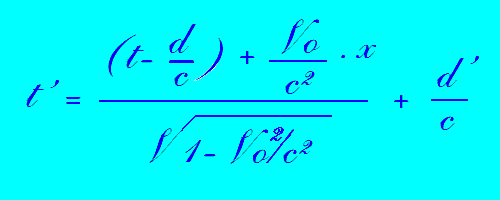
On peut alors passer de R---->R'---->R" et ainsi de suite.
Ou directement de R---->R" (en passant pas la loi d'additions de vitesses relativistes)