- - -
VI. La roue relativiste
L'un des paradoxes les plus difficiles à comprendre (et donc à expliquer) dans la théorie
de la relativité non-rectiligne est sans nul contexte le paradoxe de la roue relativiste.
Le plus souvent, le novice (voire l'érudit) va s'embourber dans ces choses en quantités de paradoxes
dont nous allons voir qu'ils n'ont pourtant pas lieu de se poser.
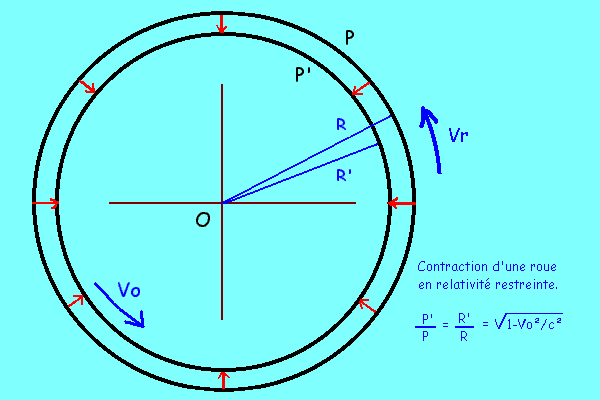
En effet; on va faire tourner de plus en plus vite une roue de rayon R,de périmètre P et de surface S connus,
et l'on va observer ce qui va se passer pour celle-ci,
lorsqu'elle est étudiée par elle même, et par un observateur neutre:
c'est à dire placé assez loin de la roue sur son axe de rotation.
On imagine alors un petit morceau de sparadrap long de 1 cm placé sur la tranche de la roue, tout en périphérie.
On admet que ce morceau de sparadrap collé sur la roue, tourne, pour lui même,
à une vitesse réelle tangentielle de Vr=0.75c
Il vient alors que, pour l'observateur externe, la vitesse tangentielle sera de Vo=0.6c
et que le morceau de sparadrap lui paraitra mesurer 0.8cm comme nous l'avons vu en relativité rectiligne.
Ceci dit, il n'est plus cohérent de dire que le périmètre reste identique à lui même.
Si, au moins, la vitesse tangentielle est bien celle que nous indiquons (Vo=0.6c),
eh bien l'ensemble du périmètre, qui n'est jamais que la somme des n bouts de sparadraps mesurant désormais 8 mm
va évidemment varier comme P'=P.sqrt(1-Vo^2/c^2).
Il y a donc contraction du cercle par le dedans, un peu comme une chambre à air extrémement gonflée
voit son diamètre diminuer lorsqu'on la dégonfle progressivement.
Il semble donc que pour le sparadrap, c'est à dire pour la roue dans son référentiel,
il n'y a pas de contraction des distances,
et que lui même (et elle même) se voient réellement évoluer à vitesse 0.75c (*)
mais que, pour l'observateur extérieur, hé bien la roue parait se contracter vers le dedans,
pendant que son rayon devient:

et son périmètre (ou un simple segment du périmètre):

On voit aussi, dans le même ordre d'idée, que la vitesse réelle tangentielle de la roue dans R'
est liée à cette même vitesse dans R selon:
Vo=Vr/sqrt(1+Vr^2/c^2)
(*)Simplement, si la roue ne se contracte nullement, et garde pour elle la même superficie,
l'espace extérieur va lui paraitre se dilater circulairement dans le plan de celle-ci,
et de façon non homogène.
A noter que le bout de sparadrap externe, qui arrive sur la roue fixe,
et qui mesure donc 0.8 cm, paraitra, pour la roue, en mesurer un lorsque tournera la roue,
puisque l'espace extérieur lui paraitra, pour elle, dilaté.
Par contre, et hormis cette dilatation spatiale du laboratoire observée par la roue
et cette contraction de la roue observée par le laboratoire, tout cela dans le plan de la roue,
il faut préciser qu'il n'y a aucune contration ou dilatation antéro-postérieure à prévoir ou à s'imaginer.
Maintenant peut disparaitre le paradoxe de la différence de longueur des deux sparadraps
tels que nous les avions déjà présentés dans cette expérience de pensée.
En effet, nous avions imaginé un autre sparadrap arrivant à la même vitesse (Vo=0.6c)
par le bas, puis se joindre à l'autre au moment où celui passe en position trois heures,
accomplissant, de façon identique à l'autre, un quart de cercle pour se libérer en position midi,
et continuant tangentiellement son chemin.
Il est clair, maintenant, que ce deuxième sparadrap sera toujours vu
selon une longueur apparente de 0.8cm, comme l'autre qui reste sur la roue,
et qu'ils peuvent même être parfaitement interchangeables.
La pointe du raisonnement qui fait tomber
tout l'édifice du brouillard conceptuel qu'il pouvait y avoir,
c'est de se dire que pour l'observateur, la roue se contracte vers l'intérieur;
mais que, pour la roue, et pour les deux sparadraps, c'est l'espace extérieur (notre référentiel) qui se dilate,
et de façon non homogène, (alors qu'elle, hormis sa rotation, elle ne bouge pas d'un pouce).
Par ailleurs, la surface observable par l'observateur externe du disque sera,
si Sr est la surface de départ, et Vo la vitesse tangentielle obtenue:
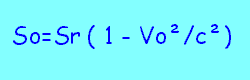
En théorie de la relativité, et lors d'un mouvement circulaire, comme ici la roue (ou le disque)
les contractions des distances et les dilatations des temps deviennent réels.
Nous avions vu que ce n'était pas le cas en relativité rectiligne,
où les référentiels étaient égaux entre eux, et où tout rapport n'était provoqué que par l'apparence.
Ici, il n'y a plus d'apparence, c'est clair, car le disque tourne réellement dans l'espace initial,
dans le référentiel initial, et non l'inverse.
Par ailleurs, la dilatation des temps est bien celle que nous attendions.
To=Tr/sqrt(1-Vo^2/c^2)
où Vo est la vitesse tangentielle observable.
-----
Maintenant, nous allons nous intéresser à ce qui va se produire selon la position concentrique sur la roue.
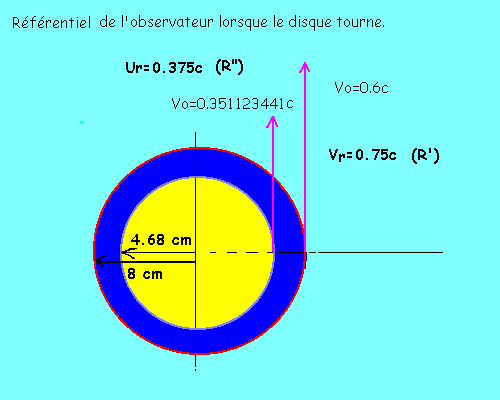
Nous allons prendre une roue de 10 cm de rayon, soit 20 cm de diamètre,
soit 62.8 cm de périmètre, soit 314 cm² environ de surface.
Lorsque la roue ne tourne pas, le référentiel de la roue est le même que celui du laboratoire,
et l'observateur et la roue notent les mêmes mesures.
Bien sûr, pour les deux, l'hémi-rayon vaut 5 cm, et la partie médullaire de la roue,
limitée par ce rayon, à un périmètre de 31.4 cm
et une surface de 78.5 cm², en vert sur les shémas.

Maintenant, nous allons faire tourner la roue,
de telle sorte que la vitesse tangentielle atteigne 0.6c dans le référentiel de l'observateur.
Ce qui veut dire que, dans le référentiel de la roue,
la vitesse tangentielle est de 0.75c.
Ici, quelque chose d'important est a considérer.
C'est que la vitesse tangentielle de l'hémicercle, mesurée un point du périmètre
va être la moitié de celle de la roue, mais rien de plus.
Nous voulons dire par là qu'il faut considérer
que le temps ne passe pas de la même façon pour le rayon, et pour l'hémirayon;
bref, que le temps passe plus lentement là où ça tourne plus vite.
Ainsi, pour un point placé à la périphérie bleue de la roue, la vitesse est de 0.75c,
alors que la vitesse que ce point percevra d'un autre point de la périphérie médullaire (verte)
sera de 0.375c, mais le temps (la vitesse de rotation des aiguilles) lui paraitra passer plus vite en médullaire.
A l'inverse, un point de la périphérie médullaire, qui va se voir tourner à Vr=0.375c
va voir la partie périphérique tourner à 0.75c, mais les aiguilles de ses horloges tourner moins vite
que les siennes propres.

Ainsi, chose capitale, il faut considérer que si le temps passe à une vitesse constante
pour tous les points du laboratoire, eh bien il en est de même pour tous les points du disque !!!
Ainsi, dans le référentiel de la périphérie du disque qui tourne,
la vitesse tangentielle est bien Vr=0.75c,
et celle du cercle médullaire est bien 0.375c.
Et réciproquement, bien que les deux horloges ne tournent pas de la même façon.
Si l'on donne une durée arbitraire To dans R, le référentiel du laboratoire,
la durée correspondante dans R' référentiel du périmètre de la roue sera:
Tr(p)=To.sqrt(1-Vo^2/c^2) ou encore: Tr(p)=To/sqrt(1+Vr^2/c^2)
et la durée correspondante dans R" référentiel du périmètre de l'hémidisque:
Tr(h)=To.sqrt(1-Uo^2/c^2) ou encore: Tr(h)=To/sqrt(1+Ur^2/c^2)
Soit un temps qui passera moins vite en R" qu'en R' selon:
Tr(h)=Tr(p).sqrt[(1-Uo^2/c^2)/(1-Vo^2/c^2)]
Ou encore:
Tr(h)=Tr(p).sqrt[(1+Vr^2/c^2)/(1+Ur^2/c^2)]
Nous allons maintenant nous mettre à la place de l'observateur.
Nous avons dit, souvenez-vous, que le rayon et le périmètre allaient se contracter selon:
R'=R.sqrt(1-Vo^2/c^2)
P'=P.sqrt(1-Vo^2/c^2)
et que la surface deviendrait:
S'=S.(1-Vo^2/c^2)
Ainsi, pour l'observateur, le rayon de la roue devient 8 cm.
Son périmètre 50.24cm; sa surface 200.96 cm²
Et la partie médullaire de la roue parait avoir pour références:
Une vitesse tangentielle de Uo=0.351123441c et un rayon de 4.68cm.
On constate alors une chose infiniment logique,
c'est que le rayon ne se contracte pas de façon constante,
mais que la partie corticale se contracte beaucoup plus que la partie médullaire.
Plus la roue tourne vite, et plus cette différence est grande.
De la même façon, plus la roue est grande, c'est à dire plus on lui ajoute
d'épaisseur de couronnes, et plus ces couronnes se contractent, pour tendre vers une surface infime
au fur et à mesure qu'on y ajoute des couches,
et faire en sorte que la vitesse observable tangente ne puisse dépasser la vitesse de la lumière.
Ainsi, pour clore:
Pour un point du périmètre de la roue (dans le référentiel spatial du labo):
la vitesse externe sera de 0.75c et la vitesse interne de:
Ur'=Ur.sqrt[(1+Vr^2/c^2)/(1+Ur^2/c^2)]=0.375*sqrt[(1+0.75²)/(1+0.375²)]=0.438904302c
Par contre, la vitesse de la périphérie bleue, pour la périphérie verte, qui se mesure à 0.375c sera:
Vr'=Vr.sqrt[(1+Ur^2/c^2)/(1+Vr^2/c^2)]=0.64080028c
Vérification:
On doit avoir R1/Vr=R2/Ur' et R2/Ur=R1/Vr'
Ou encore (R1.Ur')/(R2.Vr) = 1
et d'autre part (R2.Vr')/R1.Ur) =1
C'est exactement ce qui se passe, et le lecteur pourra le vérifier.
R1=8cm
R2=4.681645889cm
Vr=0.75c
Ur=0.375c
Vr'=0.64080028c
Ur'=0.438904302c
_______________


